Variational Coin Toss
Variational inference is all the rage these days, with new interesting papers coming out almost daily. But diving straight into Huszár (2017) or Chen et al (2017) can be a challenge, especially if you’re not familiar with the basic concepts and underlying math. Since it’s often easier to approach a new method by first applying it to a known problem I thought I’d walk you through variational inference applied to the classic “unfair coin” problem.
If you like thinking in code you can follow along in this Jupyter notebook.
The Usual Bayesian Treatment of an Unfair Coin
Okay, so we got the usual problem statement: You’ve found a coin in a magician’s pocket. Since you found it in a magician’s pocket you’re not sure it’s a “fair coin”, i.e. one that has a 50% chance of landing heads up when you toss it; it could be a “magic” coin, one that comes up heads with probability $z$ instead.
So you toss the coin a few times and it comes up tails, heads, tails, tails and tails. What does that tell you about $z$? Let’s bring out the (hopefully) familiar Bayesian toolbox and find out.
Choosing a Prior
First we need to place a prior probability distribution over $z$. Since we found the coin in a magician’s pocket we think that $z$ may very well be quite far from $0.5$. At the same time; there’s nothing obviously strange about the coin, so it seems improbable that $z$ would be very high or very low. We therefore choose $p(z) = \text{Beta}(\alpha = 3, \beta = 3)$ as our prior.
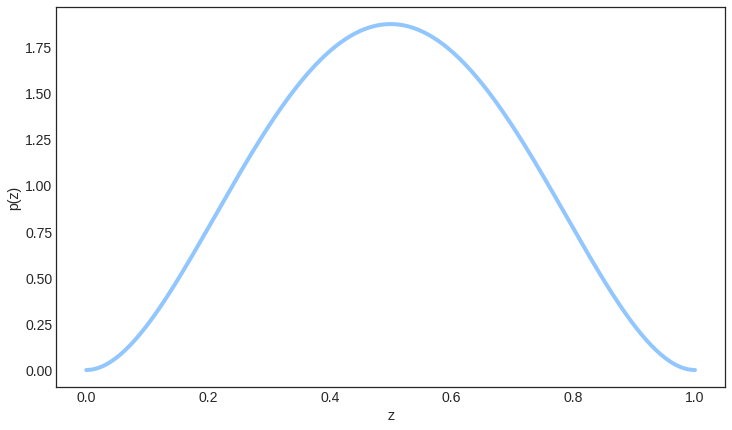
Figure 1. Prior probability distribution over $z$.
Classic Bayesian Inference
Now that we have a prior over $z$ and we’ve tossed the coin a few times we’re ready to infer the posterior. Call the outcome of the coin tosses $\vect{x}$. Then according to Bayes theorem the posterior $p(z \given \vect{x})$ is
$$ \begin{equation} p(z \given \vect{x}) = \frac{p(\vect{x} \given z) p(z)}{p(\vect{x})}, \end{equation} $$
where $p(\vect{x} \given z)$ is usually referred to as the “likelihood of $z$” and $p(\vect{x})$ is called the model “evidence”. $p(z)$ is of course just the prior.
With our choice of prior over $z$, and conditional probability of $\vect{x}$ given $z$, we could quite easily derive a closed form expression for the posterior. But since the subject here is variational inference we’ll instead see if we can approximate the posterior using variational methods.
Variational Approximation of the Posterior
The basic idea behind variational inference is to turn the inference problem into a kind of search problem: find the distribution $q^\ast(z)$ that is the closest approximation of $p(z \given \vect{x})$. To do that we of course need some sort of definition of “closeness”. The classic one is the Kullback-Leibler divergence:
$$ \begin{equation} \KL{q(z)}{p(z \given \vect{x})} = \int q(z) \log \frac{q(z)}{p(z \given \vect{x})} dz \end{equation} $$
The Kullback-Leibler divergance is always positive or zero, and it’s only zero if $q(z) = p(z \given \vect{x})$ almost everywhere.
Let’s see what happens if we replace $p(z \given \vect{x})$ in Eq. 2 with the expression derived in Eq. 1:
$$ \begin{equation} \KL{q(z)}{p(z \given \vect{x})} = \int q(z) \log \frac{q(z) p(x)} {p(\vect{x} \given z) p(z)} dz \end{equation} $$
Since $\log ab = \log a + \log b$ and $\log \frac{1}{a} = -\log a$ we can rewrite that as
$$ \begin{equation} \KL{q(z)}{p(z \given \vect{x})} = \int q(z) \log \frac{q(z)}{p(z)} dz + \\ \int q(z) \log p(\vect{x}) dz - \int q(z) \log p(\vect{x} \given z) dz. \end{equation} $$
The first term on the right hand side is (by definition) the Kullback-Leibler divergence between the prior $p(z)$ and the variational posterior $q(z)$. The second term is just $\log p(\vect{x})$, since $\log p(\vect{x})$ is independent of $z$ and can be brought out of the integral, and because the integral $\int q(z) dz$ is $1$ by definition (of probability density function). The third term can be interpreted as the expectation of $\log p(\vect{x} \given z)$ over $q(z)$. We then get
$$ \begin{equation} \KL{q(z)}{p(z \given \vect{x})} = \KL{q(z)}{p(z)} + \\ \log p(\vect{x}) - \Expect{z \sim q(z)}{\log p(\vect{x} \given z)}. \end{equation} $$
Now all we have to do is vary $q(z)$ until $\KL{q(z)}{p(z \given \vect{x})}$ reaches its minimum, and we will have found our best approximation $q^\ast(z)$! Typically that’s done by choosing a parameterized family of probability distributions and then finding the optimal parameters with some sort of numerical optimization algorithm.
Beta distribution as Variational Posterior
We start by assuming that $q(z)$ is a beta distribution, parameterized by $\alpha_q$ and $\beta_q$.
Figure 2. The beta distribution is a family of continuous probability distributions defined on the interval [0, 1], parametrized by two positive shape parameters $\alpha$ and $\beta$.
We can then derive expressions for each of the terms in Eq. 5. We start with the Kullback-Leibler divergence between the variational posterior $q(z)$ and the prior $p(z)$. Since both are beta distributions there is a closed form expression for their KL divergence
$$ \begin{equation} \KL{q(z)}{p(z)} = \log \frac{B(3, 3)}{B(\alpha_q, \beta_q)} + (\alpha_q - 3) \psi(\alpha_q) + \\ (\beta_q - 3) \psi(\beta_q) + (3 - \alpha_q + 3 - \beta_q) \psi(\alpha_q + \beta_q), \end{equation} $$
where $B$ is the beta function and $\psi$ is the digamma function.
Then the expectation of $\log p(\vect{x} \given z)$: First, we formulate $p(\vect{x} \given z)$ assuming that $x_i$ is $1$ if the $i$th coin toss came up heads and $0$ if it came up tails as
$$ \begin{equation} p(\vect{x} \given z) = \prod z^{x_i} (1 - z)^{1-x_i}, \end{equation} $$
and the logaritm of that is then
$$ \begin{equation} \log p(\vect{x} \given z) = \sum ( x_i \log z + (1-x_i) \log (1 - z) ). \end{equation} $$
Let’s call the number of heads in $\vect{x}$ $n_h = \sum x_i$ and the number of tails $n_t = \sum (1 - x_i)$. Now, since $\mathbb{E}$ is a linear operator we can write the third and final term of Eq. 5 as
$$ \begin{equation} \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} = n_h \Expect{z \sim q(z)}{\log z} + n_t \Expect{z \sim q(z)}{\log (1 - z)}. \end{equation} $$
Again, we’re lucky because there is a closed form expression for this expectation:
$$ \begin{equation} \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} = n_h (\psi(\alpha_q) - \psi(\alpha_q + \beta_q)) + \\ n_t (\psi(\beta_q) - \psi(\alpha_q + \beta_q)) \end{equation} $$
Now we’re ready to put it all together as
$$ \begin{equation} \KL{q(z)}{p(z \given \vect{x})} = \log \frac{B(3, 3)}{B(\alpha_q, \beta_q)} + (\alpha_q - 3 - n_h) \psi(\alpha_q) + \\ (\beta_q - 3 - n_t) \psi(\beta_q) + (3 - \alpha_q + 3 - \beta_q + n_h + n_t) \psi(\alpha_q + \beta_q) + \\ \log p(\vect{x}), \end{equation} $$
and go look for $\alpha^\ast_q$ and $\beta^\ast_q$ that minimize $\KL{q(z)}{p(z \given \vect{x})}$. In this very simple example there’s probably a closed form solution, but since we’re here to learn about the case when there’s not we’ll go right ahead and minimize the above expression numerically. The video below shows scipy.optimize.minimize() going to work on the problem. Note that $\log p(\vect{x})$ is independent of $\alpha_q$ and $\beta_q$ and can thus be left out of the optimization.
Figure 3. Process of finding our variational posterior $q^\ast(z)$ through numerical optimization of the closed form expression in Eq. 11.
Numerical Approximation of Difficult Integrals
As you can see from Eq. 5 variational inference is about optimization over quite hairy integrals. One thing you’ll hear a lot in this context is “we approximate the integral through Monte Carlo sampling”. What that means is essentially that we make the following approximation:
$$ \begin{equation} \int p(x) f(x) dx = \Expect{x \sim p(x)}{f(x)} \approx \frac{1}{K} \sum_{i=0}^{K} \left[ f(x_i) \right]_{x_i \sim p(x)} \end{equation} $$
Expressed in words what we do is to draw $K$ i.i.d. samples $x_i$ from the probability distribution $p(x)$ and compute the value of $f(x_i)$ for each one. We then take the average of that and call it our Monte Carlo approximation. Simple!
In this case we were quite lucky that there was a closed form expression for $\KL{q(z)}{p(z)}$ (see Eq. 6). But let’s for a moment pretend that there wasn’t. If we then go back to Eq. 5 and apply Monte Carlo approximation we get
$$ \begin{equation*} \KL{q(z)}{p(z \given \vect{x})} = \KL{q(z)}{p(z)} + \log p(\vect{x}) - \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} = \\ \Expect{z \sim q(z)}{\log \frac{q(z)}{p(z)}} + \log p(\vect{x}) - \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} \approx \\ \frac{1}{K} \sum_{i=0}^{K} \left[ \log \frac{q(z_i)}{p(z_i)} \right]_{z_i \sim q(z)} + \log p(\vect{x}) - \frac{1}{K} \sum_{i=0}^{K} \left[ \log p(\vect{x} \given z_i) \right]_{z_i \sim q(z)} = \\ \frac{1}{K} \sum_{i=0}^{K} \left[ \log q(z_i) - \log p(z_i) - \log p(\vect{x} \given z_i) \right]_{z_i \sim q(z)} + \log p(\vect{x}), \end{equation*} $$
where $q(z)$ is parameterized by $\alpha_q$ and $\beta_q$ (so we could write it as $q(z; \alpha_q, \beta_q)$ if we wanted to be very verbose in our notation). If we approximate $\KL{q(z)}{p(z \given \vect{x})}$ like this and then let scipy.optimize.minimize() go to work on finding optimal $\alpha^\ast_q$ and $\beta^\ast_q$ we get the video below. As you can see the approximation is no longer perfect, but still pretty good.
Figure 4. Process of finding our variational posterior $q^\ast(z)$ through numerical optimization of a Monte Carlo approximation of $\KL{q(z)}{p(z \given \vect{x})}$.
Normal Distribution as Variational Posterior
Beta distributed priors and posteriors are a pretty natural choice when we’re talking about coin tosses, but most of the time we’re not. In many cases we have no real reason to choose one family of distributions over another, and then often end up with normal distributions - mostly because they are easy to work with.
There’s however nothing in the variational framework that requires the prior $p(z)$ and the variational posterior $q(z)$ to come from the same family. To drive that point home we’ll switch to a normal distribution for $q(z)$, parameterized with $\mu_q$ and $\sigma_q$, while leaving $p(z)$ as $\text{Beta}(3, 3)$. Eq. 5 still holds and we can still approximate it with Monte Carlo sampling as above:
$$ \begin{equation*} \KL{q(z)}{p(z \given \vect{x})} = \KL{q(z)}{p(z)} + \log p(\vect{x}) - \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} \approx \\ \frac{1}{K} \sum_{i=0}^{K} \left[ \log q(z_i) - \log p(z_i) - \log p(\vect{x} \given z_i) \right]_{z_i \sim q(z)} + \log p(\vect{x}) \end{equation*} $$
Here $q(z)$ is really a function of $\mu_q$ and $\sigma_q$ as well (i.e. it could be written $q(z; \mu_q, \sigma_q)$ if we were really verbose in our notation), and we can find their approximately optimal values through (derivative-free) numerical optimization as we have done previously. But let’s step it up a notch and instead bring in numerical optimization workhorse numero uno: stochastic gradient descent.
For SGD to work we need to be able to differentiate $\KL{q(z)}{p(z \given \vect{x})}$ with respect to the unknown parameters $\vect{\theta_q} = (\mu_q, \sigma_q)$:
$$ \begin{equation*} \frac{\partial}{\partial \vect{\theta_q}}\KL{q(z)}{p(z \given \vect{x})} = \frac{\partial}{\partial \vect{\theta_q}} \KL{q(z)}{p(z)} + \frac{\partial}{\partial \vect{\theta_q}} \log p(\vect{x}) - \frac{\partial}{\partial \vect{\theta_q}} \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} \end{equation*} $$
Of course, since $\log p(\vect{x})$ does not depend on $\vect{\theta_q}$ its derivative is zero. $\frac{\partial}{\partial \vect{\theta_q}} \KL{q(z)}{p(z)}$ can often be computed analytically, and often even automatically e.g. by theano.tensor.grad(). But in this case where the prior $p(z)$ and the variational posterior $q(z)$ are from different families of distributions we’ll have to resort to approximation, so we use the definition of Kullback-Leibler divergence and merge the first and third term into a single expectation:
$$ \begin{equation*} \frac{\partial}{\partial \vect{\theta_q}}\KL{q(z)}{p(z \given \vect{x})} = \frac{\partial}{\partial \vect{\theta_q}} \Expect{z \sim q(z)}{ \log q(z) - \log p(z) - \log p(\vect{x} \given z)} \end{equation*} $$
Now remember that $q(z)$ is a normal distribution with mean $\mu_q$ and standard deviation $\sigma_q$. We can therefore express $z$ as a deterministic function of a gaussian noise variable $\epsilon$: $z = \mu_q + \sigma_q \epsilon$ where $\epsilon \sim \text{N}(0, 1)$. This allows us to take the expectation over $\epsilon \sim \text{N}(0, 1)$ instead:
$$ \begin{equation*} \frac{\partial}{\partial \vect{\theta_q}}\KL{q(z)}{p(z \given \vect{x})} = \frac{\partial}{\partial \vect{\theta_q}} \Expect{\epsilon \sim \text{N}(0, 1)}{ \log q(\mu_q + \sigma_q \epsilon) - \\ \log p(\mu_q + \sigma_q \epsilon) - \log p(\vect{x} \given z = \mu_q + \sigma_q \epsilon)} \end{equation*} $$
That perhaps doesn’t look like a step forward, but since we are now taking the expectation over a distribution that does not depend on $\vect{\theta_q}$ we can safely exchange the order of the derivation and the expectation operators. This maneuver is what’s commonly referred to as the “reparametrization trick”.
After reparametrization we can approximate the gradient of the Kullback-Leibler divergence between our variational posterior and the true posterior with respect to the variational parameters $\vect{\theta_q}$ using Monte Carlo sampling:
$$ \begin{equation*} \frac{\partial}{\partial \vect{\theta_q}}\KL{q(z)}{p(z \given \vect{x})} = \Expect{\epsilon \sim \text{N}(0, 1)}{ \frac{\partial}{\partial \vect{\theta_q}} \left( \log q(\mu_q + \sigma_q \epsilon) - \\ \log p(\mu_q + \sigma_q \epsilon) - \log p(\vect{x} \given z = \mu_q + \sigma_q \epsilon) \right)} \approx \\ \frac{1}{K} \sum_{i=0}^{K} \left[ \frac{\partial}{\partial \vect{\theta_q}} \left( \log q(\mu_q + \sigma_q \epsilon_i) - \log p(\mu_q + \sigma_q \epsilon_i) - \log p(\vect{x} \given z = \mu_q + \sigma_q \epsilon_i) \right) \right]_{\epsilon_i \sim \text{N}(0, 1)} \end{equation*} $$
The gradient there may look pretty ugly, but computing partial derivatives like that is what frameworks like Theano or TensorFlow do well. You just express your objective function as the average of $K$ samples from $\left[ \log q(\mu_q + \sigma_q \epsilon_i) - \log p(\mu_q + \sigma_q \epsilon_i) - \log p(\vect{x} \given z = \mu_q + \sigma_q \epsilon_i) \right]_{\epsilon_i \sim \text{N}(0, 1)}$ and call theano.tensor.grad() on that. Easy-peasy.
With $K = 10$ samples to approximate the gradient the search for $q^\ast(z)$ progresses as in the video below. As you can see there are two kinds of error in our approximation this time: as usual we’re not finding the exact optimal parameters $\mu^\ast_q$ and $\sigma^\ast_q$, but also - even if we did the variational posterior $q^\ast(z) = \text{N}(\mu^\ast_q, \sigma^\ast_q)$ would not perfectly match the true posterior $p(z \given \vect{x})$.
Figure 5. Process of finding our variational posterior $q^\ast(z) = \text{N}(\mu^\ast_q, \sigma^\ast_q)$ through stochastic gradient descent on $\KL{q(z)}{p(z \given \vect{x})}$.
Evidence Lower Bound (ELBO)
Up until now we’ve been talking about minimizing $\KL{q(z)}{p(z \given \vect{x})}$, mostly because I feel that makes intuitive sense. But in the literature it’s much more common to talk about maximizing something called the evidence lower bound (ELBO).
Thankfully the difference is minimal. We start from Eq. 5 and derive an expression for (the logarithm of) the evidence $p(\vect{x})$:
$$ \begin{equation} \log p(\vect{x}) = \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} - \KL{q(z)}{p(z)} + \\ \KL{q(z)}{p(z \given \vect{x})} \end{equation} $$
Now we observe that $\KL{q(z)}{p(z \given \vect{x})}$ must be positive or zero (because a Kullback-Leibler divergence always is). If we remove this term we thus get a lower bound on $\log p(\vect{x})$:
$$ \begin{equation} \log p(\vect{x}) \geq \Expect{z \sim q(z)}{\log p(\vect{x} \given z)} - \KL{q(z)}{p(z)} = \mathcal{L}(\vect{\theta_q}) \end{equation} $$
This $\mathcal{L}(\vect{\theta_q})$ is what is often referred to as the evidence lower bound (ELBO). Maximizing $\mathcal{L}(\vect{\theta_q})$ will give us the same variational posterior as minimizing $\KL{q(z)}{p(z \given \vect{x})}$.
But phrasing variational inference as maximization of the ELBO admittedly has at least one conceptual advantage: it shows how close we are to maximum likelihood estimation. It seems inference in the Bayesian regime is a balancing act between best explaining the data and “keeping it simple”, by staying close to the prior. If we strike the second requirement our posteriors collapse onto the maximum likelihood estimate (MLE) and we are back in the Frequentist regime.
Where to Next?
If you feel comfortable with the basics above I highly recommend Kingma and Welling’s classic paper “Autoencoding Variational Bayes”.
Any and all feedback is greatly appreciated. Ping me on Twitter or, if it’s more specific and/or you need more than 130 characters, post an issue on GitHub.
